자, 이제 빨리 DFS의 반대 개념인 BFS에 대해 배워보죠.
BFS는 너비 우선 탐색(breadth-first search)의 약자고, 역시 컴포넌트의 모든 정점을 한 번씩 순회하는 용도입니다.
DFS와 대립되는 성질을 갖고 있으며, 사용되는 곳도 매우 다릅니다.
그러나 DFS와 겹치는 용도가 있는데, BFS 역시 컴포넌트의 개수를 세거나 각 컴포넌트의 크기를 구하는 데는 사용 가능합니다.
DFS가 깊이를 중시했던 것에 반해 BFS는 넓이를 중시한다는데요.
DFS는 한 우물만 계속 파다가 끝을 보고 나서야 다른 곳으로 옮기는 데 반해, BFS는 모든 곳을 똑같이 조금씩 조금씩 팝니다.
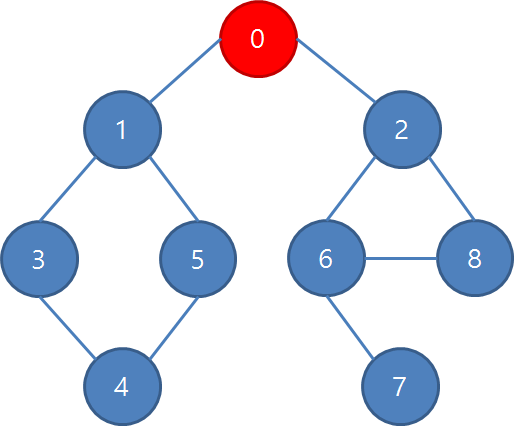
저번과 동일한 그래프를 예로 들어봅시다.
맨 처음에 0번 정점부터 방문을 시작했을 때, 그 다음 단계에는
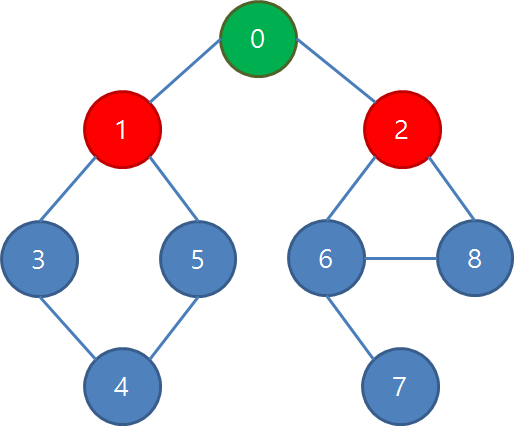
DFS에서와는 다르게, 0번 정점과 인접한 정점들부터 무조건 먼저 다 방문됩니다.
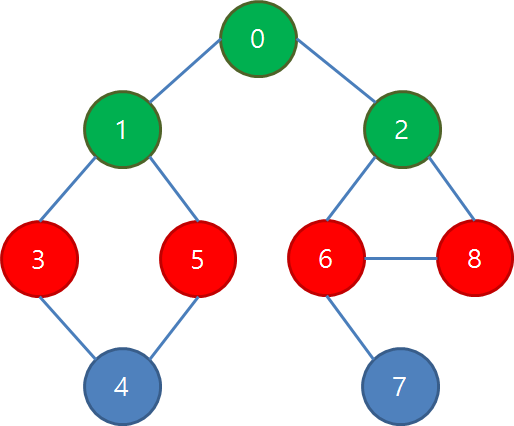
그 다음은 바로 전 단계에서 방문한 1, 2번 정점들로부터 인접한 3, 5, 6, 8번 정점들이 반드시 먼저 방문됩니다.
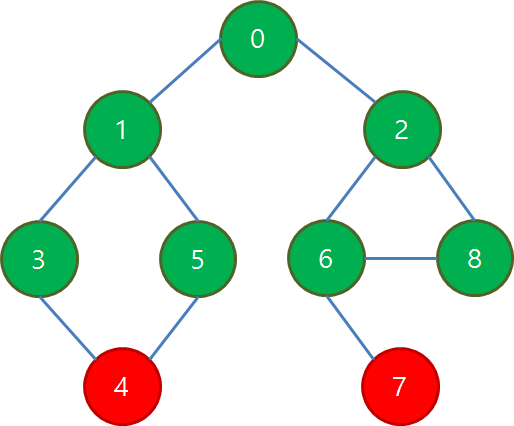
마지막으로 4, 7번 정점이 방문됩니다.
각 단계의 정점들은 그 안에서 방문 순서가 바뀔 수는 있지만, 다른 단계와는 방문 순서가 절대 뒤섞이지 않습니다.
여기서 0번 노드, 즉 시작점을 방문한 것을 0단계라 하고 그 다음부터 1, 2, 3단계라고 부를 때, k단계에 방문하는 정점들은 시작점으로부터 최단거리가 k입니다.
최단거리라 함은, 여기서는 가중치도 없으니까 A와 B의 최단거리는 A에서 B로 이동하는 데 필요한 최소 개수의 간선이라고 보시면 되겠습니다.

가운데부터 BFS를 시작했다고 할 때, 색이 얕아지는 쪽으로 퍼져가면서 탐색을 하는 모양새가 되겠습니다.
이게 마치 물방울이 물 표면에 튀겼을 때 파장이 이는 모양과 유사합니다.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 | #include <iostream> #include <vector> #include <queue> #include <algorithm> using namespace std; class Graph{ public: int N; // 정점의 개수 vector<vector<int>> adj; // 인접 리스트 // 생성자 Graph(): N(0){} Graph(int n): N(n){ adj.resize(N); } // 간선 추가 함수 void addEdge(int u, int v){ adj[u].push_back(v); adj[v].push_back(u); } // 모든 리스트의 인접한 정점 번호 정렬 void sortList(){ for(int i=0; i<N; i++) sort(adj[i].begin(), adj[i].end()); } // 너비 우선 탐색 void bfs(){ vector<bool> visited(N, false); // 방문 여부를 저장하는 배열 queue<int> Q; Q.push(0); visited[0] = true; // 탐색 시작 while(!Q.empty()){ int curr = Q.front(); Q.pop(); cout << "node " << curr << " visited" << endl; for(int next: adj[curr]){ if(!visited[next]){ visited[next] = true; Q.push(next); } } } } }; int main(){ Graph G(9); G.addEdge(0, 1); G.addEdge(0, 2); G.addEdge(1, 3); G.addEdge(1, 5); G.addEdge(3, 4); G.addEdge(4, 5); G.addEdge(2, 6); G.addEdge(2, 8); G.addEdge(6, 7); G.addEdge(6, 8); G.sortList(); G.bfs(); } | cs |
BFS를 구현해 봅시다.
DFS에 스택이 필요했던 것과 대조적으로, BFS는 큐가 필요합니다.
DFS에서 최근에 방문한 노드들부터 보는 것과 반대로, BFS는 먼저 방문한 노드들부터 보기 때문임을 아시겠나요?
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | // 너비 우선 탐색 void bfs(){ vector<bool> visited(N, false); // 방문 여부를 저장하는 배열 queue<int> Q; Q.push(0); visited[0] = true; // 탐색 시작 while(!Q.empty()){ int curr = Q.front(); Q.pop(); cout << "node " << curr << " visited" << endl; for(int next: adj[curr]){ if(!visited[next]){ visited[next] = true; Q.push(next); } } } } | cs |
BFS 함수만 떼어놓고 봅시다. 먼저 시작점을 큐에 넣고 방문했다고 표시합니다.
그리고 큐가 비어 있지 않을 때까지 방문을 시도합니다!
큐에서 지금 나온 정점의 인접한 노드들 중 아직 방문하지 않은 애들을 다시 큐에다 넣어주는 것이죠.
이런 식으로 먼저 방문한 노드들부터 차례대로 방문해 나가는 겁니다.
1 2 3 4 5 6 7 8 9 | node 0 visited node 1 visited node 2 visited node 3 visited node 5 visited node 6 visited node 8 visited node 4 visited node 7 visited | cs |
결과입니다.
컴포넌트별로 다 방문하는 건 저번처럼 이 bfs() 함수를 큰 반복문으로 감싸면 됩니다. 정점들을 순회하면서 방문하지 않은 정점들을 볼 때마다 BFS를 시작해주면 되죠.
이번에 중요한 건 그보다도, 깊이를 알아내는 겁니다.
아까 말씀드렸듯이 BFS를 잘 하면 각 노드마다 시작점으로부터의 거리를 알 수 있습니다! 이걸 어떻게 하면 좋을까요?
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 | // 너비 우선 탐색 void bfs(){ vector<bool> visited(N, false); // 방문 여부를 저장하는 배열 queue<int> Q; Q.push(0); visited[0] = true; // 탐색 시작 int level = 0; while(!Q.empty()){ int qSize = Q.size(); cout << "------ level " << level << " ------" << endl; for(int i=0; i<qSize; i++){ int curr = Q.front(); Q.pop(); cout << "node " << curr << " visited" << endl; for(int next: adj[curr]){ if(!visited[next]){ visited[next] = true; Q.push(next); } } } level++; } } | cs |
변형된 BFS 함수입니다. 하나의 더 큰 반복문으로 탐색 부분을 감쌌는데요.
먼저 현재 큐 크기를 보고, 그 큐의 크기만큼 안쪽 반복문을 반복하는 겁니다!
K번째 단계가 끝났을 때의 큐 크기는 K번째 단계에서 새로 방문하기 위해 큐에 넣은, K+1번째 단계에 방문할 노드의 개수가 됩니다.
매 단계마다 처음에 있던 만큼의 정점만 다 방문하고요.
1 2 3 4 5 6 7 8 9 10 11 12 13 | ------ level 0 ------ node 0 visited ------ level 1 ------ node 1 visited node 2 visited ------ level 2 ------ node 3 visited node 5 visited node 6 visited node 8 visited ------ level 3 ------ node 4 visited node 7 visited | cs |
결과입니다. 이제 각 정점이 0번 노드로부터 얼마나 떨어져 있는지도 알 수 있습니다.
게다가 최대 거리가 3이라는 정보를 통해서, 0번 노드로부터 가장 먼 거리에 있는 노드여도 그 거리는 최대 3이라는 것도 알 수가 있습니다.
BFS 또한 DFS와 마찬가지로, 인접 리스트를 사용하였을 때 시간복잡도가 O(V+E)입니다.
이렇게 BFS는 탐색은 하되 각 정점의 최단거리를 재야 할 때 요긴하게 쓰입니다.
'Algorithm > DFS,BFS' 카테고리의 다른 글
| BFS 문제 분석-2(촌수계산) (0) | 2018.03.18 |
|---|---|
| BFS 문제 분석-1(미로탐색) (0) | 2018.03.18 |
| DFS 문제 분석-4(텀 프로젝트 boj_9466) (0) | 2018.03.05 |
| DFS 문제 분석-4(안전영역 boj_2468) (2) | 2018.03.05 |
| DFS 문제 분석-3(영역구하기, 음식물 피하기) (0) | 2018.02.28 |

